Python基礎講座の第6回目です。
ソートアルゴリズムである「挿入ソート(Insertion Sort)」について解説します。
基本情報技術者試験にも出題される基本的なアルゴリズムなので、しっかり理解していきましょう。
挿入ソートとは
挿入ソートはソートアルゴリズムの1つです。
(ソートアルゴリズムの意味については、前回の「ソートアルゴリズムとは」で説明しています。)
名前の通りですが、挿入ソートは整列済みのデータに未整列のデータを挿入することでデータをソートするアルゴリズムです。
実際にソートの流れを見ながらのほうが分かりやすいと思いますので、[3, 8, 1, 2]を昇順にソートしながら挿入ソートのアルゴリズムを理解していきましょう。
挿入ソートでは、まず先頭の要素を整列済みと考えます。
整列済みのデータは[3]となり、未整列のデータは[8, 1, 2]です。
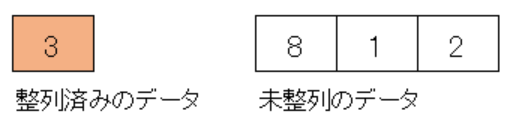
ここから未整列のデータを整列済みのデータに挿入していきます。
まずは未整列のデータの先頭にある8を整列済みのデータに挿入します。
挿入場所は以下の操作を繰り返すことで決めます。
まず整列済みのデータと未整列のデータの先頭を比較し、
- 整列済みのデータの方が大きい場合は、一つ前の整列済みデータと未整列のデータを比較する。
- 整列済みのデータの方が小さい場合は、整列済みデータの後ろに未整列のデータを挿入する。
- もし比較する整列済みデータが存在しない(先頭まできた)時は未整列のデータを先頭に挿入する。
この操作を整列済みのデータの末尾から始めます。
まず整列済みのデータの末尾である3と未整列のデータの先頭である8を比較します。

整列済みのデータの方が小さいので、整列済みデータの後ろに挿入します。

これで整列済みのデータは[3, 8]となり、未整列のデータは[1, 2]です。
次は未整列のデータの先頭にある1を整列済みのデータに挿入します。
まず整列済みのデータの末尾である8と未整列のデータの先頭である1を比較します。
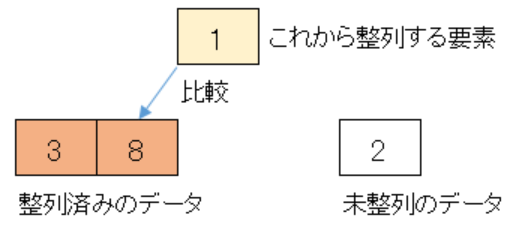
整列済みのデータの方が大きいので、一つ前の整列済みデータ3と比較します。
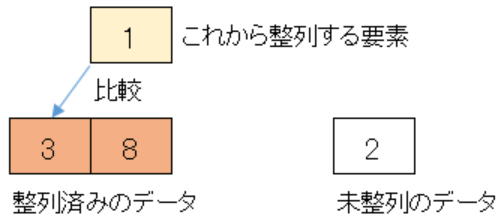
整列済みのデータの方が大きいので、一つ前の整列済みデータと比較します。
しかし整列済みデータ3より前にデータはありません。
比較する整列済みデータがなくなったため、先頭に挿入します。

これで整列済みのデータは[1, 3, 8]となり、未整列のデータは[2]です。
次は未整列のデータの先頭にある2を整列済みのデータに挿入します。
まず整列済みのデータの末尾である8と未整列のデータの先頭である2を比較します。
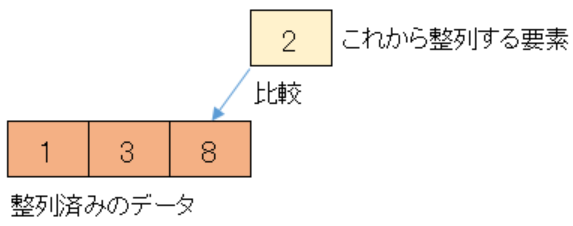
整列済みのデータの方が大きいので、一つ前の整列済みデータ3と比較します。
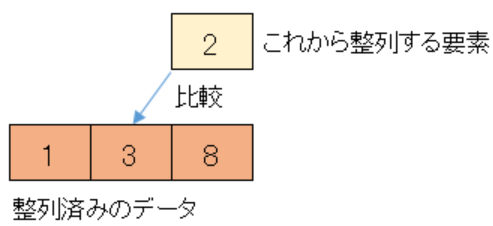
整列済みのデータの方が大きいので、一つ前の整列済みデータ1と比較します。
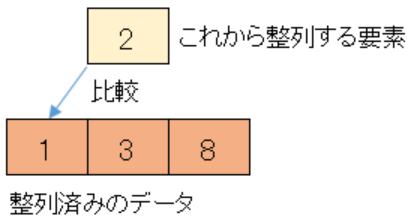
整列済みのデータの方が小さいので、整列済みデータの後ろに未整列のデータを挿入します。
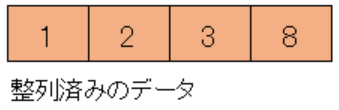
これで整列済みのデータは[1, 2, 3, 8]となり、全てのデータをソートすることができました。
このように整列済みのデータに未整列のデータを挿入することでデータをソートするアルゴリズムを挿入ソートといいます。
コード
コードにするとこのようになります。
1行ずつ確認していきましょう。
def insertion_sort(data):
length = len(data)
for index in range(1, length):
current_val = data[index]
prev_index = index - 1
while prev_index >= 0 and data[prev_index] > current_val:
data[prev_index + 1] = data[prev_index]
prev_index = prev_index - 1
data[prev_index + 1] = current_val
if __name__ == '__main__':
data = [3, 8, 1, 2, -1, -10, 4, 2]
insertion_sort(data)
print(data)コード解説
1行目
まず1行目で挿入ソートを実行するinsertion_sortメソッドを定義します。
引数にソートしたいデータ(data)を受けとります。
2行目
2行目でソートしたいデータの数をlengthに入れています。
なぜデータの数が必要か考えていきましょう。
先ほど[3, 8, 1, 2]を昇順でソートした操作をまとめてみます。
- 先頭の要素3を整列済みとする。
この時点で整列済みのデータは[3]、未整列のデータは[8, 1, 2]。 - 未整列のデータの先頭である8を整列済みデータに挿入する。
この時点で整列済みのデータは[3, 8]、未整列のデータは[1, 2]。 - 未整列のデータの先頭である1を整列済みデータに挿入する。
この時点で整列済みのデータは[1, 3, 8]、未整列のデータは[2]。 - 未整列のデータの先頭である2を整列済みデータに挿入する。
この時点で整列済みのデータは[1, 2, 3, 8]となり、全てのデータのソートが完了。
操作1は先頭の要素を整列済みとしただけでソートは行っていません。
実際にソートしているのは操作2~4ですので、[3, 8, 1, 2]のデータをソートするには3回の操作が必要となります。
つまり、4個のデータをソートするには3回の操作が必要です。
ではデータが[3, 8, 1, 2, 6]の場合は何回の操作が必要でしょうか?
この場合も同じように操作をまとめてみます。
- 先頭の要素3を整列済みとする。
整列済みのデータは[3]、未整列のデータは[8, 1, 2, 6]となる。 - 未整列のデータの先頭である8を整列済みデータに挿入する。
整列済みのデータは[3, 8]、未整列のデータは[1, 2, 6]となる。 - 未整列のデータの先頭である1を整列済みデータに挿入する。
整列済みのデータは[1, 3, 8]、未整列のデータは[2, 6]となる。 - 未整列のデータの先頭である2を整列済みデータに挿入する。
整列済みのデータは[1, 2, 3, 8]、未整列のデータは[6]となる。 - 未整列のデータの先頭である6を整列済みデータに挿入する。
整列済みのデータは[1, 2, 3, 6, 8 ]となり、全てのデータのソートが完了。
今回も操作1は先頭の要素を整列済みとしただけでソートは行っていません。
実際にソートしているのは操作2~5ですので、[3, 8, 1, 2, 6]のデータをソートするには4回の操作が必要となります。
つまり、5個のデータをソートするには4回の操作が必要です。
もうお分かりかもしれませんが、挿入ソートでは先頭以外の要素を1つずつ挿入して整列済みとするため、先頭以外のデータの要素数がソートする回数となります。
つまりソートしたいデータの要素数とソートする回数の関係は、「ソートする回数 = ソートしたいデータの要素数 – 1」と表せます。
このように、必要な操作の回数を知るためにデータの要素数が必要なので、2行目でデータの要素数をlengthに入れています。
3行目
次に3行目でrange(1, length)の範囲でループし、操作が何回目にあたるかを index に入れています。
例えばPythonでは for index in range(1, 5):と書くことで index は1, 2, 3, 4の値をとり、4回ループします。
先ほどみたようにループの回数(操作の回数)はデータの要素数 – 1回となっています。
4行目
4行目はcurrent_val = data[index]です。
indexには1回目の操作なら1、2回目の操作なら2のように何回目の操作かを表す値が入っています。
1回目の操作ではcurrent_val =data[1]となり、2回目の操作ならcurrent_val =data[2]となります。
つまりdata[index]はこれからソートするデータを表し、その値をcurrent_valに入れています。
current_valは以下の図でいうと「これから整列する要素」を表しています。
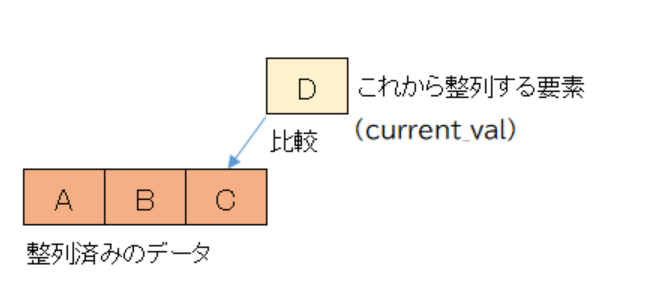
5~11行目
5~11行目は先ほど見た以下の操作を表しています。
- 整列済みのデータの方が大きい場合は、一つ前の整列済みデータと未整列のデータを比較する。
- 整列済みのデータの方が小さい場合は、整列済みデータの後ろに未整列のデータを挿入する。
- もし比較する整列済みデータが存在しない(先頭まできた)時は未整列のデータを先頭に挿入する。
詳しく見ていきましょう。
5行目のprev_indexは比較する整列済みデータの位置を表します。
最初に比較するのは整列済みデータの末尾でした。
整列済みデータの末尾はこれから整列するデータの1つ手前です。
そのためprev_index = index – 1としています。
また、比較する整列済みデータの位置は比較するたびに先頭に向かって1つ進んでいきましたね。
つまり比較するたびにprev_index = prev_index – 1 となります。
コードが少し前後しますが、これは9行目で行っています。
次は7行目のwhile文ですが、説明の関係で先ほど見た以下の操作に番号をふり、上から条件1とします。
- 整列済みのデータの方が大きい場合は、一つ前の整列済みデータと未整列のデータを比較する。
- 整列済みのデータの方が小さい場合は、整列済みデータの後ろに未整列のデータを挿入する。
- もし比較する整列済みデータが存在しない(先頭まできた)時は未整列のデータを先頭に挿入する。
結論からいうと、7行目のwhile文の処理は条件1の時だけ入るようになっています。
while文が何を意味するかを前半と後半に分けて説明していきます。
まず前半のprev_index >= 0ですが、prev_indexは比較する整列済みデータの位置を表していました。
データの位置は以下のように先頭が0から始まります。
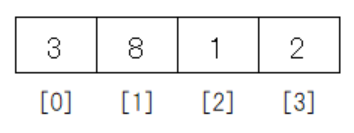
先頭データの位置が0ですから、データの位置が0より小さいというのは先頭より前になります。
比較する整列済みデータが先頭よりも前というのは、比較する整列済みデータがないということです。
これは条件3「もし比較する整列済みデータが存在しない(先頭まできた)時」です。
つまり、prev_index >= 0とすることで比較する整列済みデータが存在する場合のみwhileの処理が行われるようにしており、言い換えると条件3の時にはwhileの処理が行われないようになります。
後半のdata[prev_index] > current_valは、整列済みのデータの方が大きい場合を表しています。
つまり条件2の整列済みのデータの方が小さい場合はwhileの処理が行われないようになります。
まとめると、while prev_index >= 0 and data[prev_index] > current_valとすることで条件1の場合のみwhileの処理が行われ、条件2と3はwhileの処理が行われなくなります。
これによりwhileの中にある8行目と9行目の処理は条件1の時に実行され、whileの外にある11行目の処理は条件2と3の時に実行されるということが分かります。
9行目は先ほどprev_indexの時に説明した「比較する整列済みデータの位置は比較するたびに先頭に向かって1つ前に進む」でした。
では8行目は何をしているでしょうか。
コードを見ると整列済みデータを1つ後ろにずらしています。
まず概要を理解してほしいため先ほどの説明では省きましたが、挿入ソートでは比較した後に整列済みデータを1つ後ろにずらす操作が必要になります。
理由は挿入する場所を空けるためです。
図で見た方がイメージしやすいので図で見てみましょう。
例えば整列済みのデータが[1, 3, 8]で未整列のデータが[2]の時にどのように2が整列済みデータに挿入されるかを図で見てみます。
今回はデータの位置が分かりやすいように、それぞれのデータの位置に番号をふっています。
まず整列済みのデータの末尾である8と未整列のデータの先頭である2を比較します。
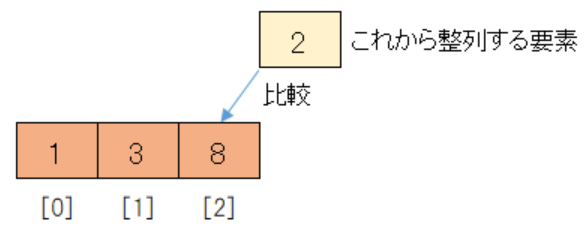
整列済みのデータの方が大きいので、一つ前の整列済みデータ3と比較するのですが、その前に8を後方に一つずらします。
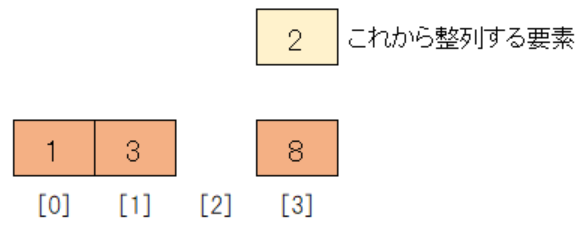
次に整列済みのデータ3と比較します。
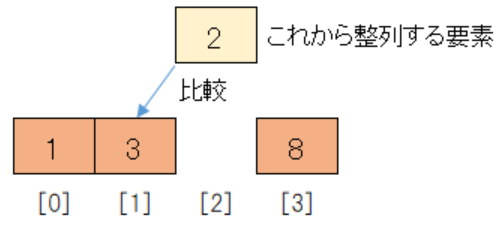
整列済みのデータの方が大きいので、3を後方に一つずらします。
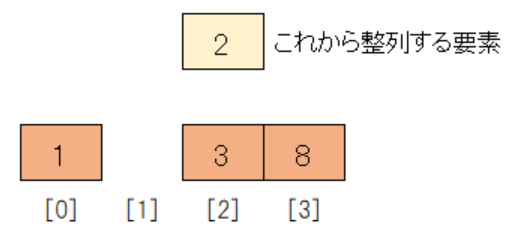
次に整列済みのデータ1と比較します。
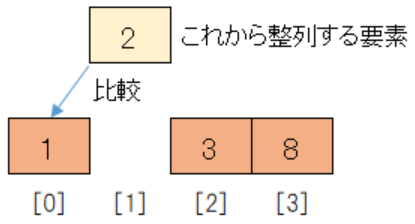
整列済みのデータの方が小さいので、整列済みデータの後ろに未整列のデータ2を挿入します。
先ほど3を後方にずらしたことで[1]が空いているため、空きスペースに挿入することができます。
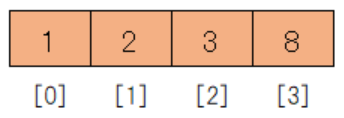
今見たように挿入するためのスペースを空けるため、8行目で整列済みデータを後方にずらしています。
最後の11行目ですが、条件2と3の共通処理でした。
条件2と3で共通となる処理は未整列データの挿入ですね。
prev_indexは比較した整列済みデータの位置を表しているため、prev_index + 1で1つ後ろの空きスペースの位置を表します。
つまり空きスペースのデータ(data[prev_index + 1])に未整列のデータ(current_val)を入れています。
実行結果
コードを実行して昇順にソートされることを確認しましょう。

ちゃんと昇順にソートされていますね。
計算量
最後にデータ数をNとした時の計算量をO記法で表現してみましょう。
(O記法については以前学んだO記法の説明を参考にしてください。)
挿入ソートのコードの中で、ソートするデータ数によって計算量が変わるところはどこでしょうか。
まず3行目のfor index in range(1, length)ですね。
forでループしており、ループ数はlengthで決まります。
lengthには2行目でデータ数(len(data))を入れているため、ループ数はデータ数によって変わります。
もう一か所あります。
それは7行目のwhile文です。
挿入ソートのアルゴリズムを少し振り返ると、未整列のデータを整列済みデータと繰り返し比較し、先頭まで繰り返すか、もしくは整列済みデータよりも未整列のデータの方が大きければ繰り返しを終了しました。
もし1度目の比較で整列済みデータよりも未整列のデータの方が大きければ繰り返しは1回だけで済みますが、整列済みデータよりも未整列のデータの方が小さい場合が続けば、操作は先頭まで繰り返されます。
この先頭まで比較を繰り返す場合を考えると、データ数がNなら比較する回数はN – 1回となります。
つまりデータ数Nが増えれば増えるほど操作の回数も増えるため、操作の回数はデータ数に比例していると考えられます。
ここまでをまとめると、計算量がデータ数に比例するのは3行目のfor文と7行目のwhile文の2か所であり、while文はfor文の中にネストしています。
(このネストした計算量の説明はバブルソートの計算量のところで解説しています。
もしよく分からなければそちらを参考にしてみてください。)
つまり挿入ソートの計算量はO(N) x O(N) = O(N2)となります。
最後に & 関連書籍
以上、第6回目は挿入ソートについてでした。
基本のアルゴリズムですので、しっかり理解しておきましょう。
以下の記事で他のソートアルゴリズムについても解説しています。
興味があれば読んでみてください。
以下では探索アルゴリズムを解説しています。
こちらも基本のアルゴリズムとなりますので、しっかり理解しておきましょう。
分かりにくいところや「もっとこうしてほしい」などのご意見がありましたら、ツイッターから連絡いただけると幸いです。
質問に関してもお気軽にお問い合わせください。
以下は関連書籍です。





コメント