Python基礎講座の第4回目です。
探索アルゴリズムである「線形探索(Linear Search)」と「二分探索(Binary Search)」について解説します。
基本情報技術者試験にも出題される基本的なアルゴリズムなので、しっかり理解していきましょう。
探索アルゴリズムとは
探索アルゴリズムは複数のデータの中から条件に一致する値を見つけるためのアルゴリズムです。
線形探索はとてもシンプルなアルゴリズムで分かりやすいです。
ですので、まず線形探索を説明し、次に二分探索を説明していきます。
線形探索 (Linear Search)
線形探索はとてもシンプルなアルゴリズムです。
単純に先頭のデータから順番に探索していき、探しているデータが見つかれば探索を終了します。
コード
def lenear_search(data, key):
for i, item in enumerate(data):
if item == key:
return i
return -1
if __name__ == '__main__':
data = [1, 3, 7, 13, 17, 21, 74]
print(lenear_search(data, 13))コード解説
短くてシンプルなコードですね。
lenear_searchメソッドの中で線形探索を行っています。
具体的には、まず2行目で引数に渡されたリスト (data) の先頭からループを使って全て探索していきます。
3行目で探しているデータ (key) と一致するか確認し、一致する場合は4行目で要素の番号 (i) を返しています。
探しているデータがリストになかった場合は5行目で-1を返します。
注意点としては、リストの番号は先頭が0からはじまります。
なので今回のコードではリストの中から13を探しており、リストの4つ目の要素が13なので結果は以下のように3となります。

線形探索のアルゴリズムがだいたい理解できたでしょうか。
せっかく理解したのなら実践でも線形探索のアルゴリズム使いたいですね。
実践で使うためには、あともう一歩。
アルゴリズムの効率を理解し、状況に合わせて早く計算が完了するアルゴリズムを選べるようにならなければなりません。
なぜならユーザーさんはボタンを押してから操作完了まで30秒待たなければいけないようなシステムを使ってくれないからです。
では一緒に線形探索アルゴリズムの効率を考えていきましょう。
O記法(オーダー記法) アルゴリズムの効率
アルゴリズムの効率は計算量で決まります。
計算量が多いアルゴリズムは効率が悪く、反対に計算量が少ないアルゴリズムは効率の良いアルゴリズムとなります。
この効率が良いかどうかをO記法 (オーダー記法) という方法で表します。
O記法とはデータ量と計算量の関係を表したものです。
今は以下の表現だけ覚えておきましょう。
面倒ですがこれは覚えるしかないです。
- O(1)
- O(logN)
- O(N)
3つの関係はそれぞれ以下のようになります。
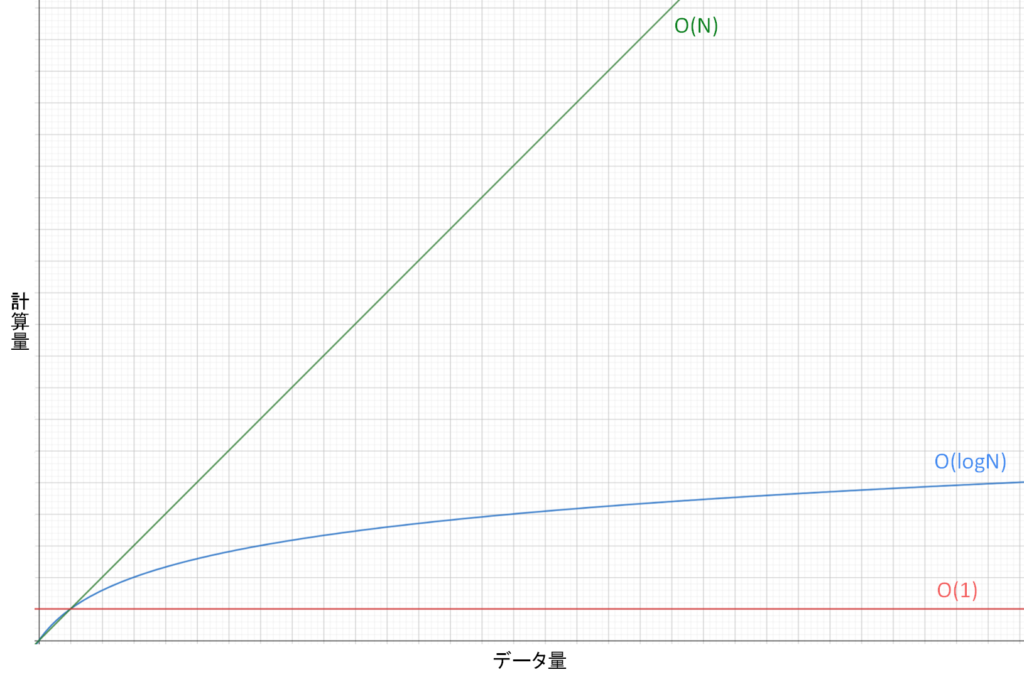
まずO(1)ですが、これはデータ量Nがどんなに増えても、探索が常に一回しか行われないという意味です。
例えば10万件のデータがあったとしても目的のデータを1回で見つけられるということです。
非常に効率が良いですね。
説明の都合上、次にO(N)を説明します。
これは計算量がデータ量Nに比例するという意味です。
y=axという式では、yはxに比例するというのを習ったことがあると思います。
私はこのイメージで、計算量=O(N)なら計算量はデータ量Nに比例すると覚えています。
最後はO(logN)です。
数学でやったかもしれませんが、これは対数ですね。
上図を見ればわかるように、データ量が増えても計算量は増えにくい特徴があります。
O(logN)はO(N)よりも計算量が少なく、効率が良いアルゴリズといえます。
まとめると、計算量の多さは以下となります。
O(1) < O(logN) < O(N)
できるだけO(N)よりもO(logN)、O(logN)よりもO(1)となるアルゴリズを使いましょう。
計算量
では本題の線形探索の計算量ですが、先ほど覚えた「O(1)、O(logN)、O(N)」のどれになるでしょうか?
線形探索ではデータを先頭から1つ1つ調べていくのでデータが増えた分だけ計算量が増えていきます。
つまり計算量はデータ量Nに比例します。
比例を表すのはO(N)でしたね。
線形探索の計算量はO(N)となります。
二分探索 (Binary Search)
二分探索は線形探索と比べてとても速いアルゴリズムになります。
ただし二分探索の使用には条件があり、探索対象のデータがソート(整列)されていないと使えません。
探索対象のデータがソートされていない場合は、まずデータを昇順(小さい順)もしくは降順(大きい順)にソートする必要があります。
この二分探索は名前から予想できますが、データを二分していくことで目的のデータを探すアルゴリズムです。
具体的には、探索対象の真ん中にあるデータと探したいデータを比較します。
データが昇順(小さい順)に並んでいるとすると、探したいデータの方が大きい場合は、探したいデータは探索対象データの後半部分にあるということですね。
なので探索対象を後半部分に絞り込みます。
逆に探したいデータの方が小さい場合は、探したいデータは探索対象の前半部分にあるということです。
この場合、探索対象を前半部分に絞り込みます。
この絞り込みを繰り返し、探索対象の真ん中にあるデータと探したいデータが一致するか、もしくは探索対象のデータが1つになった場合に探索を終了します。
コード
def binary_search(data, key):
start = 0
end = len(data) - 1
while(start <= end):
middle = (start + end) // 2
if data[middle] == key:
return middle
elif data[middle] < key:
start = middle + 1
else:
end = middle - 1
return -1
if __name__ == '__main__':
data = [1, 3, 7, 13, 17, 21, 74]
print(binary_search(data, 17))コード解説
1行目で二分探索を行うbinary_searchメソッドを定義します。
binary_searchメソッドを呼び出しているのは18行目で、引数には17行目で作成したソート完了済みのデータ (data) を渡しています。
binary_searchの中でどういう処理を行っているか解説していきます。
まず2行目のstartで探索対象のデータの先頭を指定し、3行目のendで探索対象のデータの末尾を指定します。
二分探索では探索するごとに探索対象のデータが半分に絞り込まれていきます。
このデータが半分になっていく動きは、startとendの位置を移動させることで表現します。
startとendの位置は5~13行目のwhileの中で決めていきます。
1回探索するごとにこのwhileの処理が1回行わます。
6行目のmiddleで探索対象のデータの中央の位置を指定します。
Pythonでは X // 2と書くことでXを2で割った商を求めます。
8行目で中央にあるデータ (data[middle]) が探しているデータ (key) であれば、9行目で中央の位置 (middle)を返します。
10行目では、中央にあるデータが探しているデータより小さいか確認しています。
小さければ11行目で探索対象のデータの先頭 (start) を中央の1つ後ろの位置に移動します。
中央にあるデータが探しているデータより大きい場合は12行目のelseに入ります。
その場合、探索対象のデータの末尾 (end) を中央の1つ前の位置に移動します。
探しているデータが見つかるまでこのwhileの中の操作を繰り返します。
今回のコードでは、探索対象のデータの中から17を探しています。
17はリストの5つ目にあるため、実行結果は4となっています。

計算量
探索対象のデータ量をNとします。
二分探索では探索するごとにデータ量が1/2になっていきます。
探索を繰り返しデータが1つに絞り込まれた時の探索回数をkとすると、1 = N/2kと表せます。
1=N/2kから計算していきます。
2k=N
log2k=logN
k=logN
データ量をNとした時、探索回数はlogNとなりました。
つまり二分探索の計算量はO(logN)です。
最後に & 関連書籍
以上、第4回目はPythonの基礎というよりプログラミングの基礎となりました。
基本のアルゴリズムですので、しっかり理解しておきましょう。
どのアルゴリズムがどれくらいの計算量かイメージできると更に良いです。
以下ではソートアルゴリズムを解説しています。
こちらも基本のアルゴリズムとなりますので、しっかり理解しておきましょう。
分かりにくいところや「もっとこうしてほしい」などのご意見がありましたら、ツイッターから連絡いただけると幸いです。
質問に関してもお気軽にお問い合わせください。
以下は関連書籍です。




コメント